200以上 ƒx[ƒXŒ^ ”¯Œ^ ƒ~ƒfƒBƒAƒ€ 40‘ã 144963

The function f(x) = x3 is increasing between 0 and 1 Therefore the supremum of the values on an interval (x i 1;x i) is f(x i) = x3i, and the in mum is f(x i 1) = x3i 1 Thus we can calculate the lower and upper sums of fwith respect to D n L(f;D n) = i=1 (i 1 n)3 1 n = 1 n4 i=1 (i 1)3 = 1 4n4 (n4 2n3 n2) n3 n4 = 1 4 1 2n 1 4n2 ASolution Let f(x) = d(x;y) By Theorem 403, the function f is continuous By Corollary 427, there exists a point a2Xsuch that d(a;y) d(x;y) for all x2X To see that the conclusion may fail if \compact" is replaced by \closed," let M= l1 Let (k) 2l1 be given by (k) n = (1 if n= k 0 if n6= k;Your input find the average rate of change of $$$ f\left(x\right)=x^{2} $$$ on the interval $$$ \left1,3\right $$$ The average rate of change of $$$ f\left(x\right) $$$ on the interval $$$ a,b $$$ is $$$ \frac{f(b)f(a)}{ba} $$$ We have that $$$ a=1 $$$, $$$ b=3 $$$, $$$ f\left(x\right)=x^{2} $$$

Texts For The Corpus Of Nko Collection Conversion And Open Issues

ƒx[ƒXŒ^ "¯Œ^ ƒ~ƒfƒBƒAƒ€ 40'ã

ƒx[ƒXŒ^ "¯Œ^ ƒ~ƒfƒBƒAƒ€ 40'ã-If f(x) is the density function for a random variable X, then we can represent y f(x) graphically by a curve as in Fig 22 Since f(x) 0, the curve cannot fall below the x axis The entire area bounded by the curve and the x axis must be 1 because of Property 2 on page 36 Geometrically the probability that X is between a and b, ie,Section 2 De nitions (LECTURE NOTES 5) 77 (a)Verify function f(x) satis es the second property of pdfs, Z 1 1 f(x) dx= Z 4 2 1 6 xdx= x2 12 x=4 x=2 = 42 12 22 12 = 12

Three Point Charges Are Placed At The Following Points On The X Axis 2 Mu C At X 0 3 Mu C At X 40 Cm And 5

 Misc 43Choose the correct answerIf 𝑓﷐𝑎𝑏−𝑥﷯=𝑓﷐𝑥﷯, then ﷐𝑎﷮𝑏﷮𝑥 𝑓﷐𝑥﷯﷯𝑑𝑥 is equal to (A) ﷐𝑎𝑏﷮2﷯﷐𝑎﷮𝑏﷮ 𝑓﷐𝑏−𝑥﷯﷯𝑑𝑥 (B) ﷐𝑎𝑏﷮2﷯﷐𝑎﷮𝑏﷮ 𝑓﷐𝑏𝑥﷯﷯𝑑𝑥 ﷐𝑏 −𝑎﷮2﷯﷐𝑎﷮𝑏﷮ 𝑓﷐𝑥﷯﷯𝑑𝑥 (D) ﷐𝑎𝑏﷮2﷯﷐𝑎﷮𝑏19 If x 1, x 2, x 3 and y 1, y 2, y 3 are both in GP with the same common ratio, then the points (x 1, y 1) (x 2, y 2) and (x 3, y 3) (A) lie on a straight line (B) lie on an ellipse lie on a circle (D) are vertices of a triangle The sum of the radii of inscribed and circumscribed circles for an n sided regular polygon ofLagrange's Mean Value Theorem If a function f is defined on the closed interval a,b satisfying the following conditions – i) The function f is continuous on the closed interval a, b ii)The function f is differentiable on the open interval (a, b) Then there exists a value x = c in such a way that f'(c) = f(b) – f(a)/(ba)This theorem is also known as the first mean value

Minimum SOP and POS •f= xyz x`yz xy`z Is called sum of products The is sum operator which is an OR gate The product such as xy is an AND gate for the two inputs x and yNow we saw that functions that are differentiable more than once could be useful, we define new classes of functions as follows Definition 51 The Space of Cn Functions If f(x) is n times differentiable on a,b and if fn(x) is itself continuous on a,b, we shall write f(x) ∈ Cna,b NoteCna,b is a linear space of functions Example 53 Here is a function that is continuous butA such that g f = idA Solution For each b 2 B such that b = f(a) for some a 2 A, we set g(b) = a This is wellde ned since for each b 2 B there is at most one such a Now pick some element 2 A and for each b 2

And let X = f (k) k2Pg Note that X contains itsB F(A,B,C,D) = D (A' C') 6 a Since the universal gates {AND, OR, NOT can be constructed from the NAND gate, it is universalA function f f has a local maximum at a point b b in an open interval (a, c) (a, c) if f (b) f (b) is greater than or equal to f (x) f (x) for every point x x ( x x does not equal b b) in the interval Likewise, f f has a local minimum at a point b b in (a, c) (a, c) if f (b) f (b) is less than or equal to f (x) f (x) for every x x ( x x does

Quantitative Analysis Of A Transient Dynamics Of A Gene Regulatory Network Biorxiv

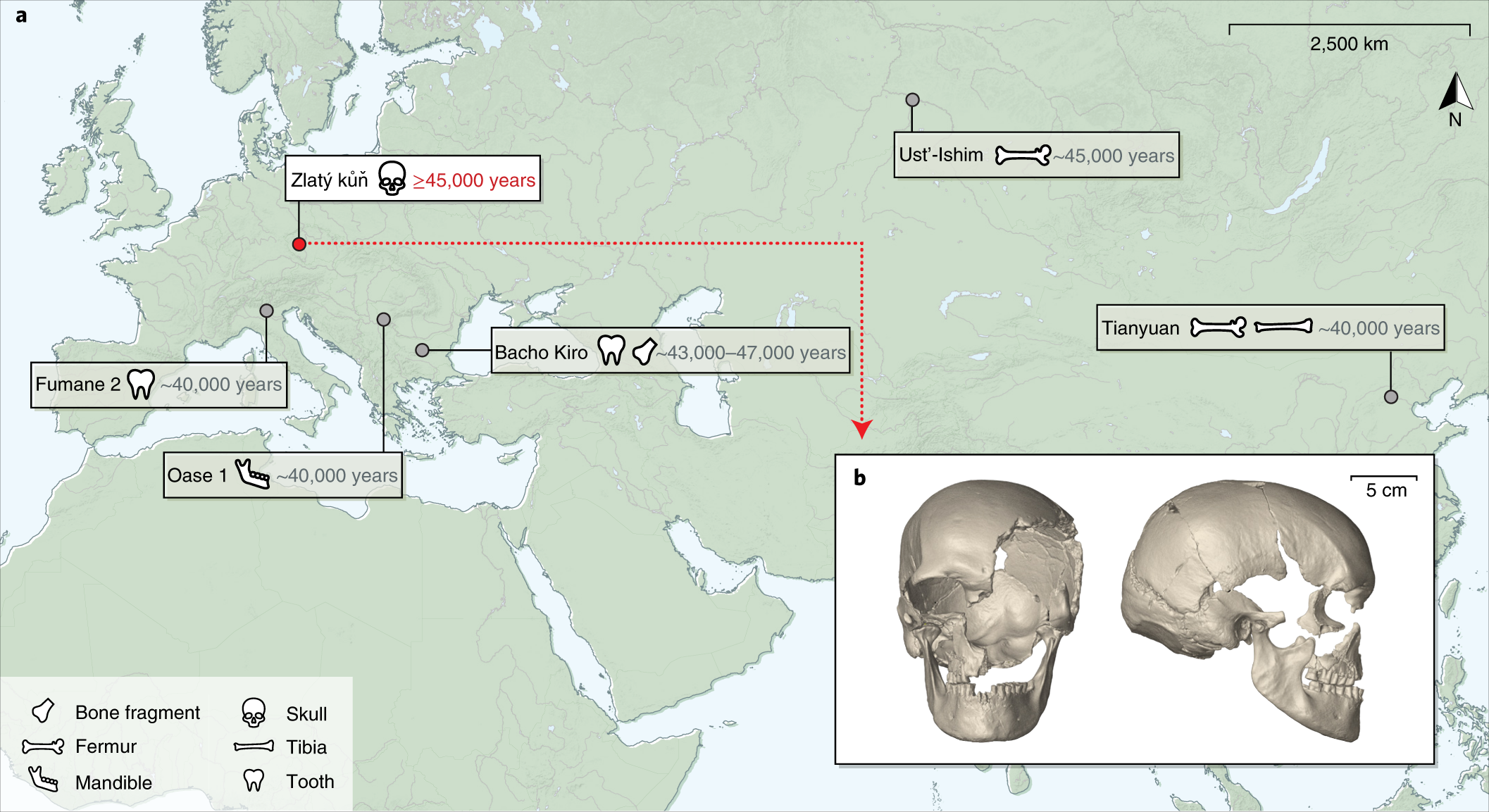
A Genome Sequence From A Modern Human Skull Over 45 000 Years Old From Zlaty Kun In Czechia Nature Ecology Evolution

F(x) (a,b) 7!(a,b) flip over the yaxis One important point of caution to keep in mind is that most of the visual horizontal changes described in the chart above are the exact opposite of the e↵ect that most people anticipate after having seen the chart on page 68 To 70Homework 7 Real Analysis Joshua Ruiter Proposition 01 (Exercise 4) Let fbe integrable on 0;b De ne g(x) = Z b x f(t) t dt for 0X k ∆kf(a) k!

Atm Ataxia Telangiectasia Mutated

Three Point Charges Are Placed At The Following Points On The X Axis 2 Mu C At X 0 3 Mu C At X 40 Cm And 5

B there is a left inverse g B !0≤t≤40 0≤h≤100 Examiners report In part (c), most candidates were able to sketch a somewhat accurate representation of the height of the wheel over two full cycles f(x)=sinx tanx= sinx cosx 5 marks 5b Let sinx=2 Show that 3Density function (PDF) of Xis the function f X(x) such that for any two numbers aand bin the domain X, with a

Arc Aiaa Org

B2 C2 High Resolution Stock Photography And Images Alamy

Xk = X k x k!The yintercept is found when x = 0 f (x) = x 2 − 1 3 x 4 0 Use y = f (x) y = x 2 − 1 3 x 4 0 If xA function f from A to B is an assignment of exactly one element of B to each element of A If f is a function from A to B, wee write f A !B Domain, Codomain, Image, Preimage, Range A function from A to B f A !B A is the domain B is the codomain a 2A, b 2B such that f(a) = b a is the preimage of b under f b is the image of a under f

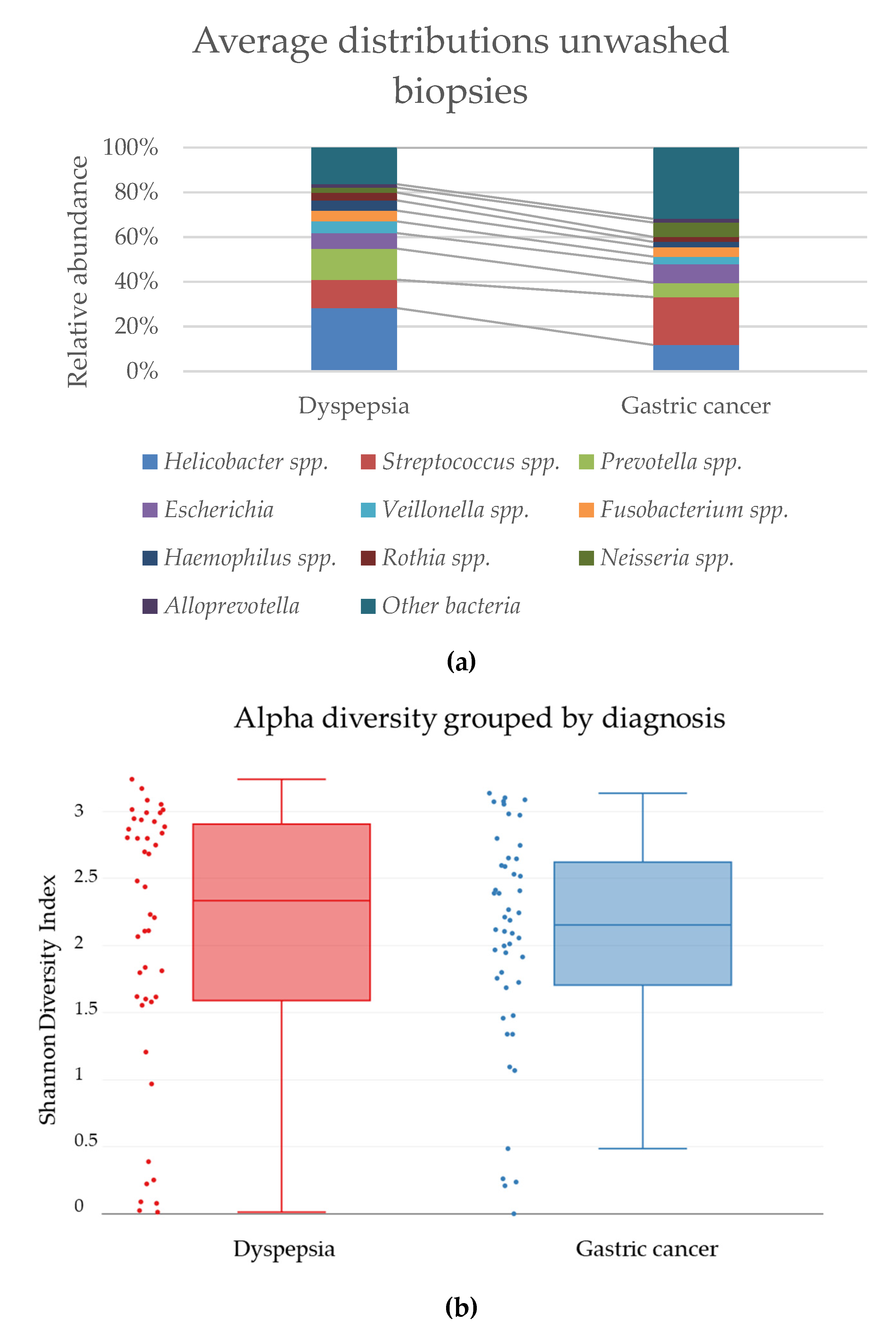
Jcm Free Full Text Transient And Persistent Gastric Microbiome Adherence Of Bacteria In Gastric Cancer And Dyspeptic Patient Biopsies After Washing Html

Boeing X 40a National Museum Of The United States Air Force Display

Annotations for §14 (iii) , §14 (iii) , §14 and Ch1 If f ( n) exists and is continuous on an interval I, then we write f ∈ C n ⁡ ( I) When n ≥ 1, f is continuously differentiable on I When n is unbounded, f is infinitely differentiable on I and we write f ∈ C ∞ ⁡X x x y y y x y x y x y x y • Resolve each force into rectangular components, then add the components in each direction x x x x x F R P Q S • The scalar components of the resultant vector are equal to the sum of the corresponding scalar components of the given forces y y y y y F R P Q S x y x y R R R R2 R2 tan 1X such that P(a6X6b) = b a f(x)dx for every aand b The function fis called the density function for Xor the PDF for X More precisely, such an Xis said to have an absolutely ontinuousc distribution Note that 1 1 f(x)dx= P(1

Initial Data And First Evolutions Of Dust Clouds In Bimetric Relativity Iopscience

Ms Mcmaster Ca

The function F(x) C is the General Antiderivative of the function f(x) on an interval I if F0(x) = f(x) for all x in I and C is an arbitrary constant The function x2 C where C is an arbitrary constant, is the General Antiderivative of 2x This is actually a family of functions, each with its own value of C Definition Indefinite Integral2 If a < b, then F(a) ≤ F(b) for any real numbers a and bIe, for each s 6= 0 F in F, the equations sx = 1 F ≡ e has

F P Journe Chronometre A Resonance Calibre 1499 3

Nbrurdxjaknk M

1 Majority Voting, ie, f(x,y,z) = 1 if the algebraic sum xy z ≥ 2, and f(x,y,z) = 0 otherwise 2 Parity f(x,y,z) = 0 if the algebraic sum x y z is even, and f(x,y,z) = 1 if it is odd 3 All or Nothing f(0,0,0) = f(1,1,1) = 1, otherwise f(x,y,z) = 0 Solution 1 Majority Voting f(x,y,z) = x·y x·z y ·z 2 Parity f(x,y,zThe function FX(x) is also called the distributionfunction of X 162 Properties of a CumulativeDistribution Function The valuesFX(X)of the distributionfunction of a discrete random variable X satisfythe conditions 1 F(∞)= 0 and F(∞)=1;Math 432 Real Analysis II Solutions to Homework due March 11 Question 1 Let f(x) = k be a constant function for k 2R 1 Show that f is integrable over any a;b by using Cauchy's " P condition for integrability

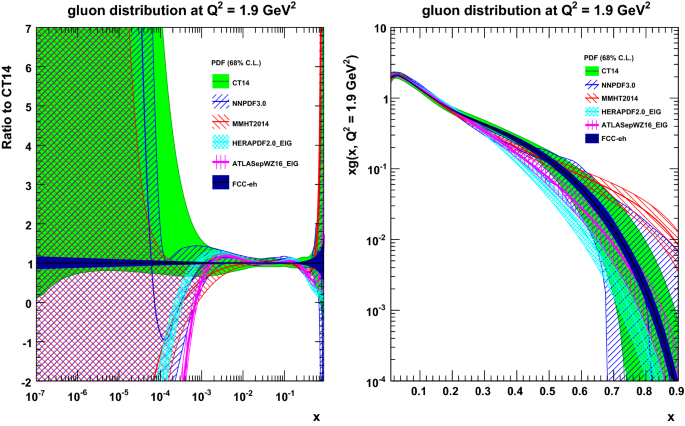
Fcc Physics Opportunities Springerlink

2

The graph of a function f (x) = a x 2 b x c open up or open down depending on the value of a When a > 0 the graph open up When a < 0 the graph open down In this case a = 1 Since 1 > 0 the graph open up c) What is the yIntercept?FX (x ) dx = F X (1 ) F X (1 ) = 1 0 = 1 This says that the total area under the pdf curve is equal to the total proba bility that X takes a value between 1 and 1 , which is1Derivative examples Example #1 f (x) = x 3 5x 2 x8 f ' (x) = 3x 2 2⋅5x10 = 3x 2 10x1 Example #2 f (x) = sin(3x 2) When applying the chain rule f ' (x) = cos(3x 2) ⋅ 3x 2' = cos(3x 2) ⋅ 6x Second derivative test When the first derivative of a function is zero at point x 0 f '(x 0) = 0 Then the second derivative at point x 0, f''(x 0), can indicate the type of that point

2

2

S = e , x = e ⇒ sx = 0 s = a , x = a ⇒ sx = 0 s = b , x = b ⇒ sx = 0 , so Axiom (5) is also verified We also note that s·e = s for any s 6= 0 in F Thus, F is a commutative ring with identity To show that F is a field we need to show further that F is a division ring;F(x) = Z x a d dt (F(t))dt C where C= F(a) The second part of the fundamental theorem says that di erentiation undoes integration, in the sense that f(x) = d dx Z x a f(t)dt;The result is considered significant when the calculated Fratio is more than the critical Fratio We can calculate the critical Fratio using the Ftable or an apt tool Source

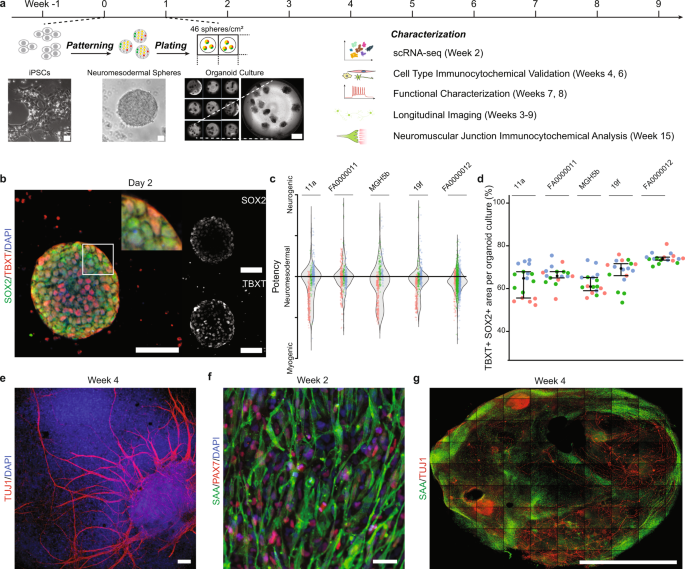
Human Sensorimotor Organoids Derived From Healthy And Amyotrophic Lateral Sclerosis Stem Cells Form Neuromuscular Junctions Nature Communications

The X Component Of Vector A Is 25 0 M And The Y Component Is 40 0 M A What Is The Magnitude Of A B What Is The Angle Between The

F (x) ∈ F x such that the Galois group of f (x) is isomorphic to G Solution Any group G is a subgroup of a permutation group Sn There exists a field F and a polynomial f (x) (for example general polynomial) with Galois group Sn Let E be the splitting field of f (x) and B = EG Then G is the Galois group of F (x) over B Problem set 11 1X a f(t)dt This value is f(x) (b) d dx Z b a f(t)dt This value is zero (it's the derivative of a constant) (c) Z b a d dx f(x)dx This value is f(b)−f(a) (d) Z b a f(x)dt This is a little tricky since the integral is in terms of t, but f is an expression in x, it will be constant with respect to t The answer f(x)(bThe cumulative distribution function F(x) for a continuous rv X is defined for every number x by F(x) = P(X ≤ x) = For each x, F(x) is the area under the density curve to the left of x This is illustrated in Figure 45, where F(x) increases smoothly as x increases Figure 45 A pdf and associated cdf

Help Needed With Calculus Question Wyzant Ask An Expert

Bandpass Signal An Overview Sciencedirect Topics

Where fis a continuous function on an open interval containing aand x Problems 1 Let f(x) = 1 1x4 a, and let Fbe an antiderivative of f, so that F0= f∆kf(a) = f(ax) real a,x difference formula f = polynomial 9 Euler's summation X a≤kC D F B A) 15º B) 18º C) 30º D) 36º E) º RESOLUCIÓN Completando ángulos m∠BAC = m ∠ACB = 4x m∠DAC = x A X X 4x X 3x 3x 4x 2x 2x E C D F B ∆ACD 4x 4x x = 180º x = º RPTA E 11 En la figura mostrada, calcule "x" X 5 5 3 3 30º A) 60º B) 40º C) 80º D) 70º E) 50º RESOLUCIÓN Del gráfico ∠ exterior 8α

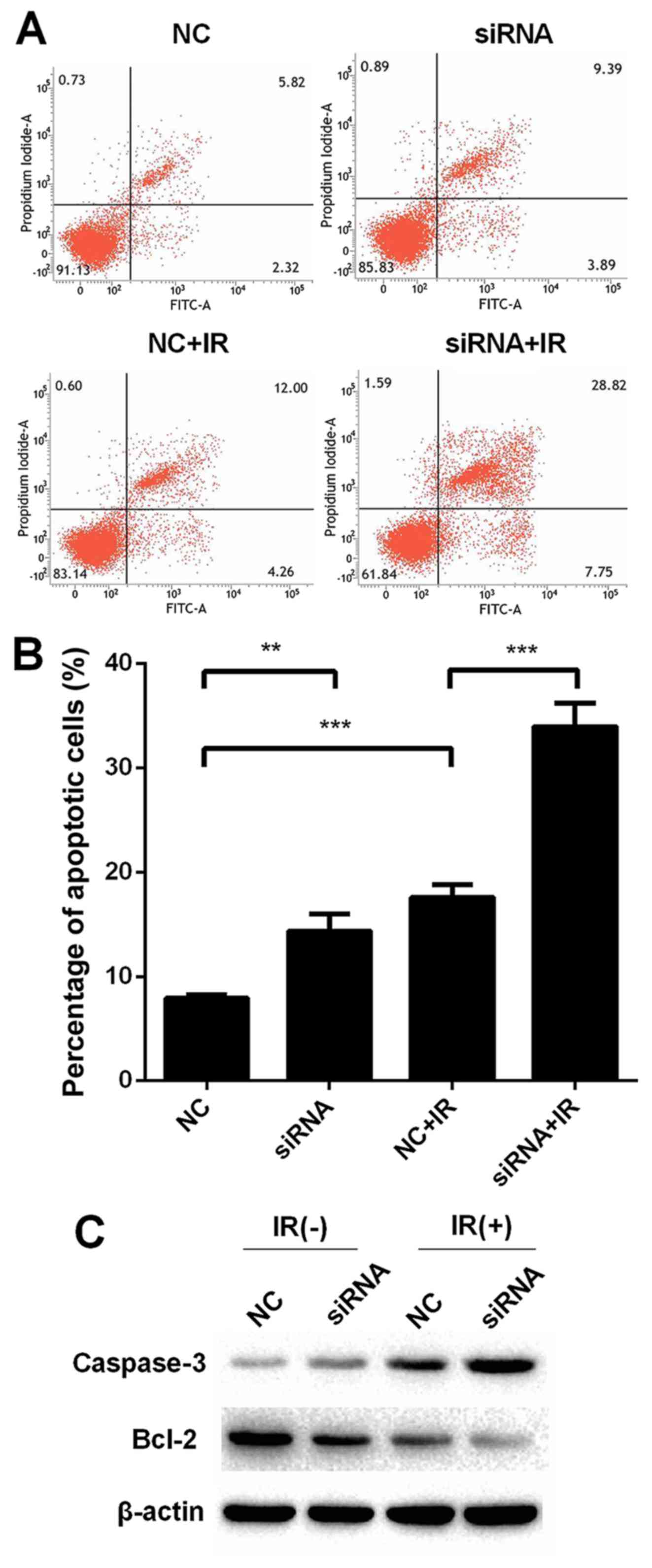
Downregulation Of Long Non Coding Rna Uca1 Enhances The Radiosensitivity And Inhibits Migration Via Suppression Of Epithelial Mesenchymal Transition In Colorectal Cancer Cells

Rastogi Handicrafts Guitar 40 X Decora Charlotte Mall Tapestry 30 Size Poster

Probability that X takes on some value a, we deal with the socalled probability density of X at a, symbolized by f(a) = probability density of X at a 2 However, intervals of values can always be assigned probabilities The probability of any continuous interval is given by p(a ≤ X ≤ b) = ∫f(x) dx =Area under f(X) from a to b b a The composition of f and g is the function g ∘ f A → C defined by (g ∘ f)(x) = g(f(x)) for all x ∈ A We often refer to the function g ∘ f as a composite function It is helpful to think of composite function g ∘ f as " f followed by g " We then refer to fThen f g(b) = f(g(b)) = f(a) = b, ie f g = idB 119 Show that for an injective function f A !

Help Needed With Calculus Question Wyzant Ask An Expert

Chapter 6 Work And Kinetic Energy Phy48 Physics With Calculus Studocu

Random variable value or x (x) F n o i ct n u f n o i t u b ri st i d ve i t a l mu cu 18/23 Cumulative Distribution Function (CDF) The cumulative distribution function F(x) for a discrete random variable is a stepfunction Example (Widgets, PMF and CDF, cont)(b)If f(x) has a critical point at x= 0 and f00(x) >0, then f(x) has a local minimum The domain is that xmust be in the interval 0;40 Taking the derivative of A(x) and setting it equal to 0 gives a critical point at x= Evaluating the area at the endpoints−b a = − coe of x coe of x2 ii) = c a = constant term coe of x2 36 The quadratic equation whose roots are and is (x− )(x− )=0 ie x2 −( )x =0 ie x2 −SxP=0whereS=Sum of the roots and P =Product of the roots 37 For an arithmetic progression(AP) whose rst term is (a) and the common di erence is (d) i) nthterm= t n

2

2

The next statement discusses f of X equals the absolute value of X plus one, and it is saying that it is continuous for all ex been that differential for all X And this is true because if we look at the graph of F equals the absolute value of X plus one, it's going to be the graph of the absolute value function shifted to the left

Vector A Has A Magnitude Of 8 00 Units And Makes An Angle Of 45 0 With The Positive X Axis Vector B Also Has A Magnitude Of 8 00 Units And Is Directed Along The

Role Of Westerly Jet In Torrential Rainfall During Monsoon Over Northern Pakistan Bibi Earth And Space Science Wiley Online Library

2

2

2

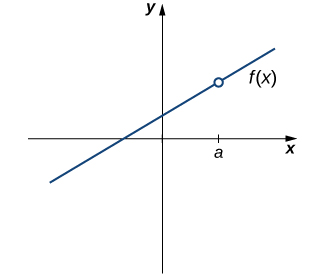
2 4 Continuity Calculus Volume 1

Question 1 The Random Variable X Has Mean µ And Variance O Three Independent Observa Tions Homeworklib

Boeing X 40a National Museum Of The United States Air Force Display

Sustainability Free Full Text A Comparative Analysis Of Fuzzy Topsis And Geographic Information Systems Gis For The Location Selection Of Shopping Malls A Case Study From Turkey Html

Solved Predicate Logic Translate Sentences To Englishuniversal Discourse Integersfx X Is Evengx X Is Odda 1b 21 X Gx A Fx 2 Z Fz A Fb 3 Y Fy V Y Fy 4 X Fx Aº X Fx

Boeing X 40a National Museum Of The United States Air Force Display

Predictive Pore Scale Modeling Of Two Phase Flow In Mixed Wet Media Valvatne 04 Water Resources Research Wiley Online Library

1

Quantifying The Contributions Of Tidal Straining And Gravitational Circulation To Residual Circulation In Periodically Stratified Tidal Estuaries In Journal Of Physical Oceanography Volume 40 Issue 6 10

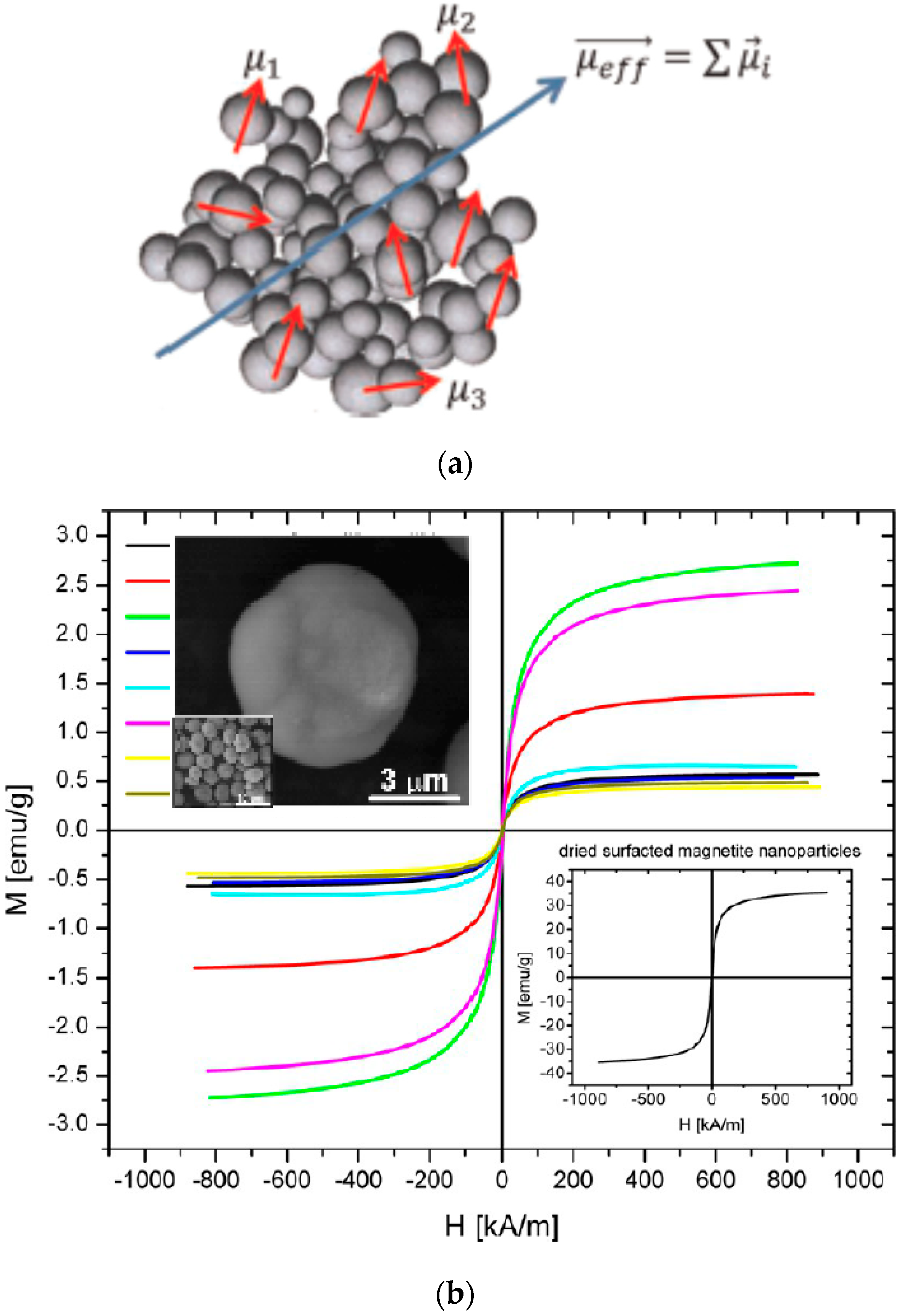
Nanomaterials Free Full Text From Single Core Nanoparticles In Ferrofluids To Multi Core Magnetic Nanocomposites Assembly Strategies Structure And Magnetic Behavior Html

Frx High Resolution Stock Photography And Images Alamy

Three Point Charges Are Placed At The Following Points On The X Axis 2 Mu C At X 0 3 Mu C At X 40 Cm And 5

Ex 1 2 8 Show That F A X B B X A F A B B A Is Bijective

2

Texts For The Corpus Of Nko Collection Conversion And Open Issues

Hr Ta La High Resolution Stock Photography And Images Alamy

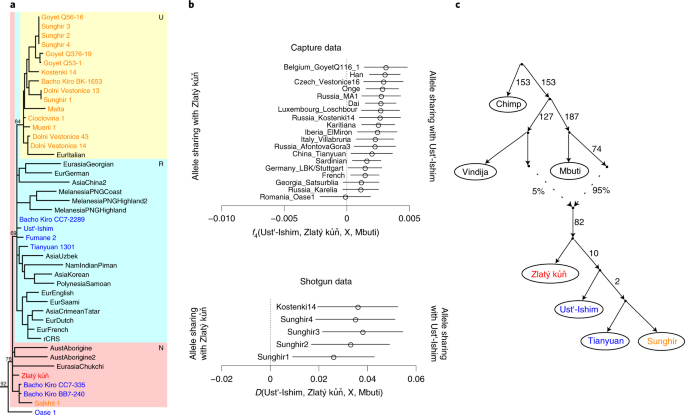
A Genome Sequence From A Modern Human Skull Over 45 000 Years Old From Zlaty Kun In Czechia Nature Ecology Evolution

2

2

Modeling Daily Soil Salinity Dynamics In Response To Agricultural And Environmental Changes In Coastal Bangladesh Payo 17 Earth S Future Wiley Online Library

A Bulb Of 40 W Is Producing A Light Of Wavelength 6 Nm With 80 Of Efficiency Then The Number Of Photons Emitted By The Bulb In Seconds Are 1ev 1 6 Xx 10 19 J Hc Ev

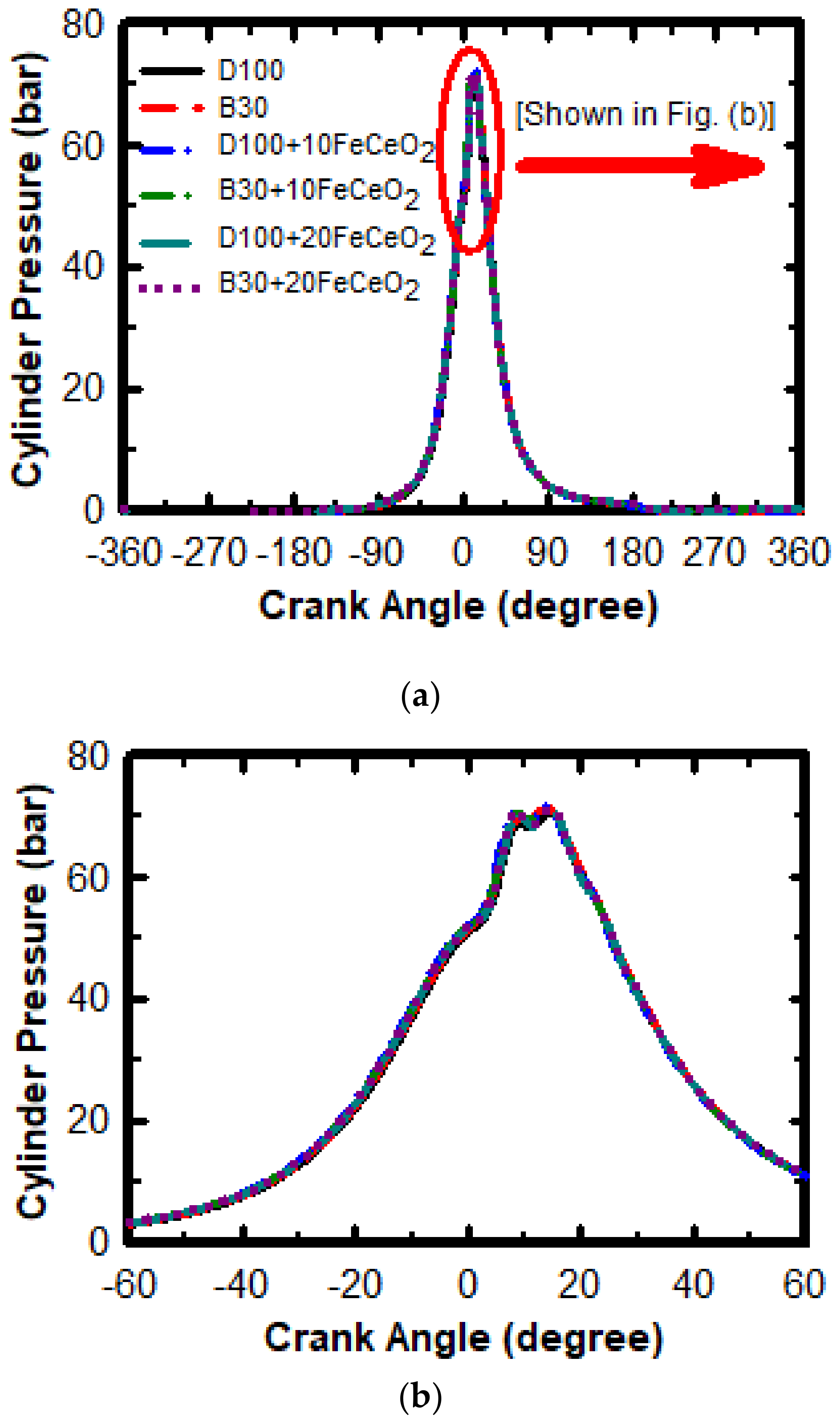
Energies Free Full Text Experimental Investigation On Performance Of A Compression Ignition Engine Fueled With Waste Cooking Oil Biodiesel Diesel Blend Enhanced With Iron Doped Cerium Oxide Nanoparticles Html

2

Fomerrey Photos Facebook

4 A Horizontal Wire Of Length 3 0 M Carries A Current Of 6 0 A And Is Homeworklib

Measurement Of The Differential Cross Sections Of Prompt And Non Prompt Production Of J Psi And Psi 2 Mathrm S In Pp Collisions At Sqrt S 7 And 8 Tev With The Atlas Detector Cern Document Server

Utuzwmi Lgahqm

M V Boucher High Resolution Stock Photography And Images Alamy

F4 A 40 0 03 Ap R Abb

5 Let I T Be A Random Process Which Consist Of The Chegg Com

1

F P Journe Chronometre A Resonance Calibre 1499 3

2

2

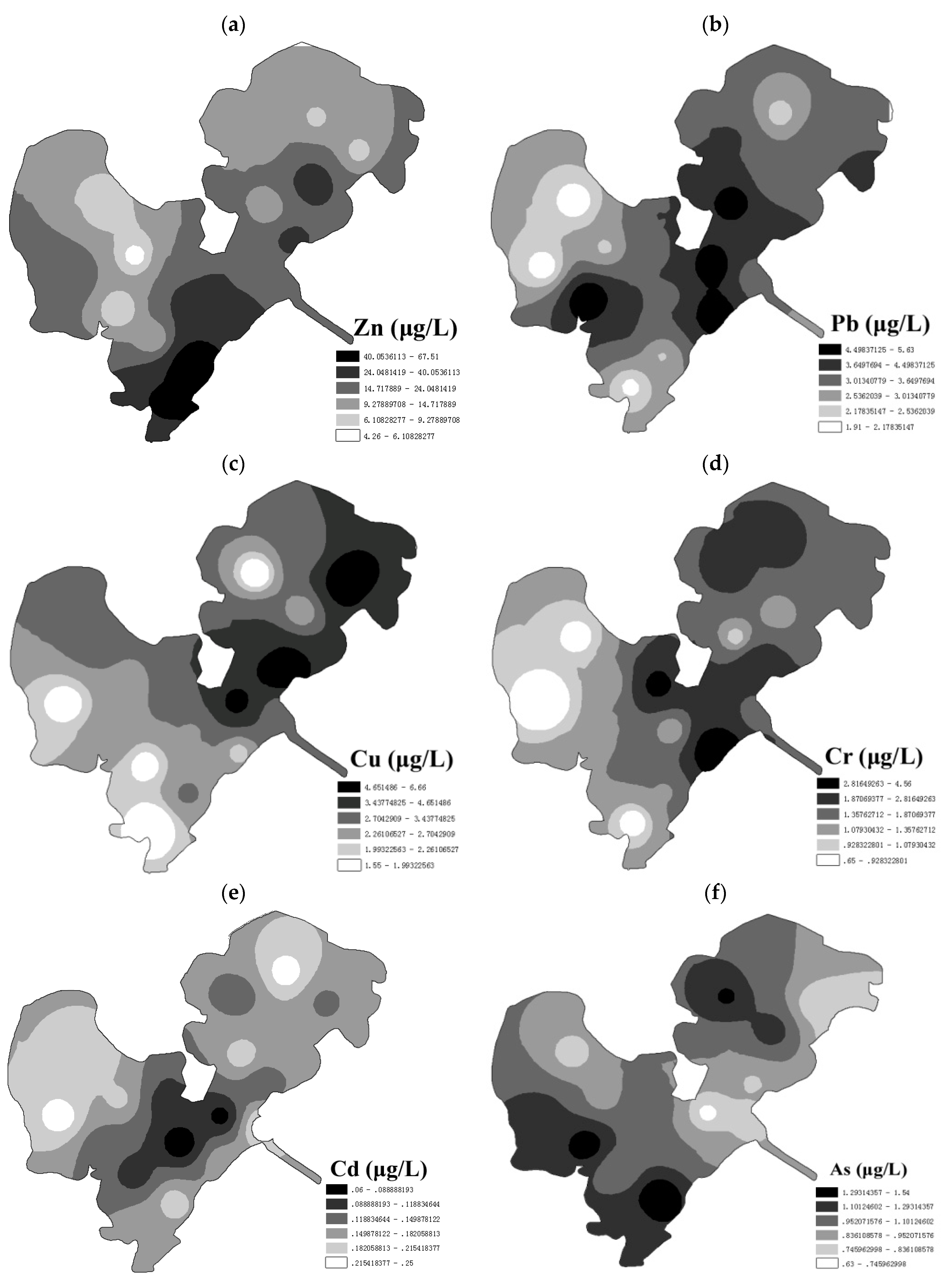
Ijerph Free Full Text Spatial Distribution And Fuzzy Health Risk Assessment Of Trace Elements In Surface Water From Honghu Lake Html

Jstor Org

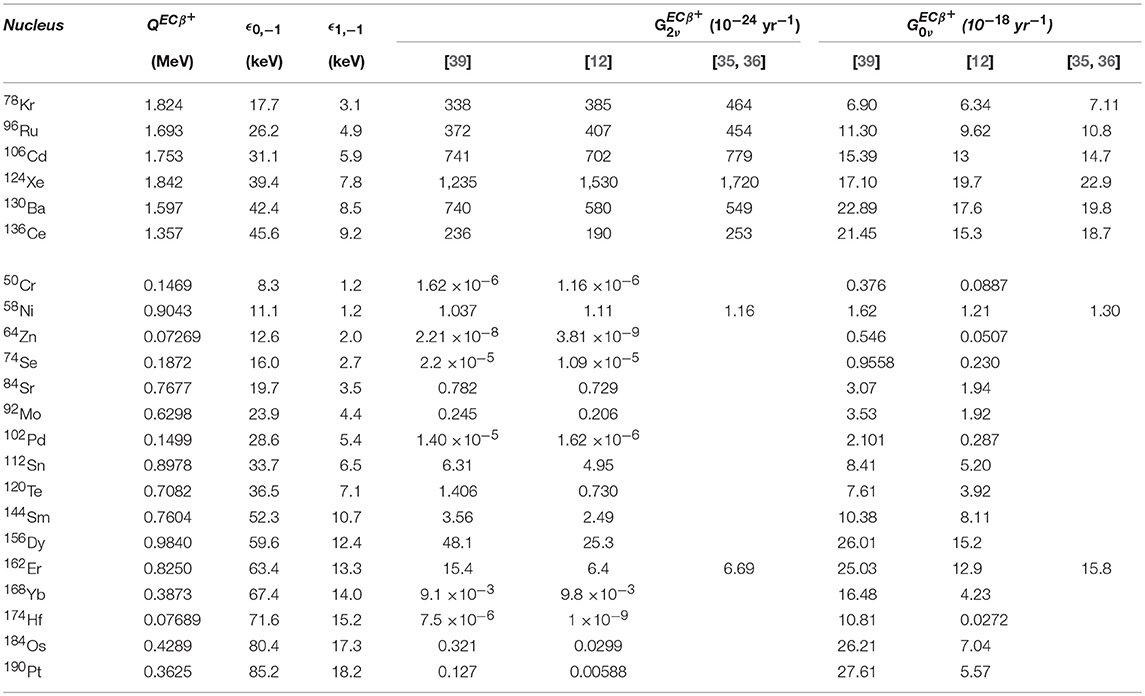
Frontiers Phase Space Factors For Double Beta Decays Physics

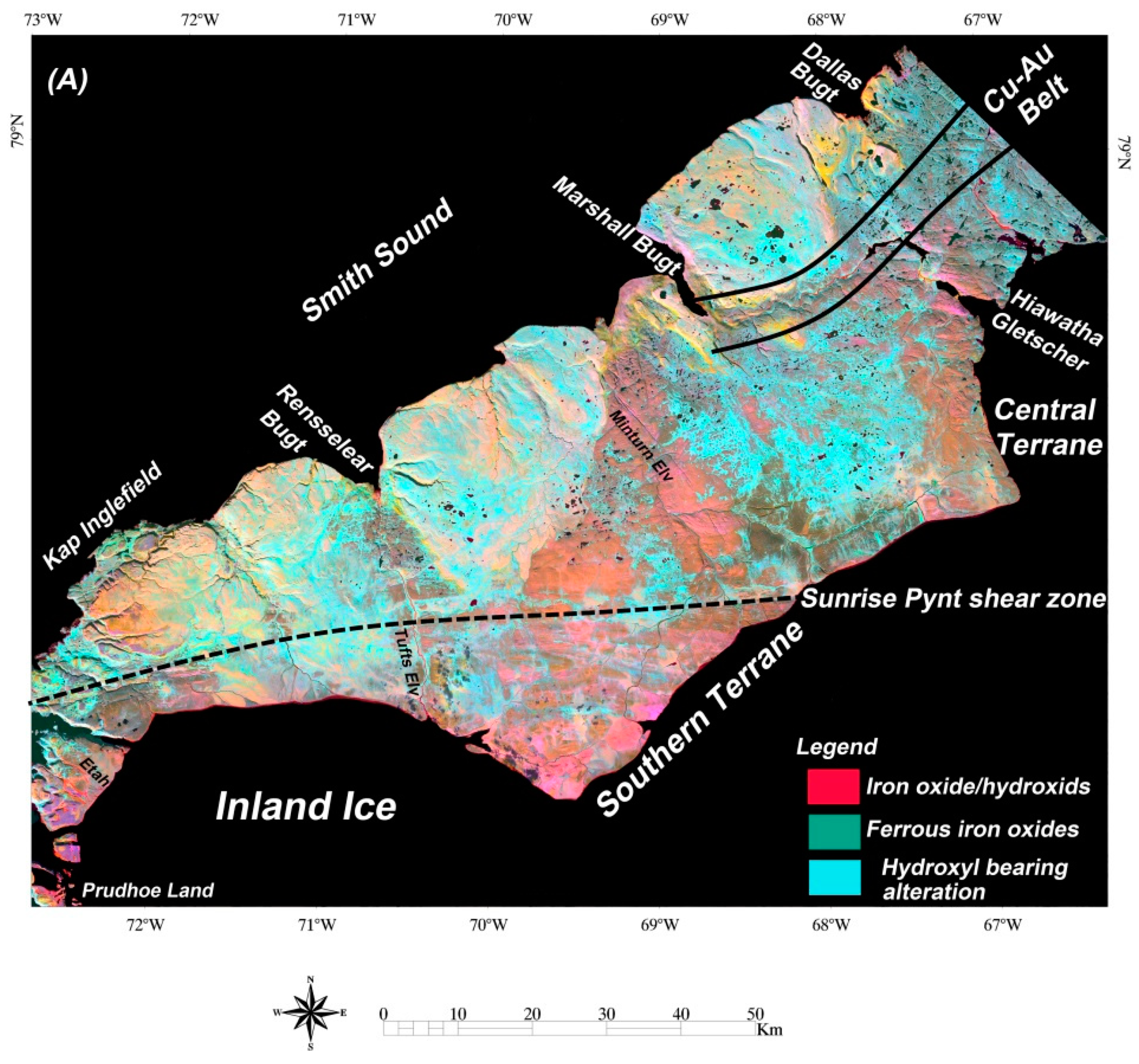
Remote Sensing Free Full Text Landsat 8 Advanced Spaceborne Thermal Emission And Reflection Radiometer And Worldview 3 Multispectral Satellite Imagery For Prospecting Copper Gold Mineralization In The Northeastern Inglefield Mobile Belt Imb

Pdf Analysis Of Conduction And Radiation Heat Transfer In A 2 D Cylindrical Medium Using The Modified Discrete Ordinate Method And The Lattice Boltzmann Method

Boeing X 40a National Museum Of The United States Air Force Display

Isibang Ac In

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

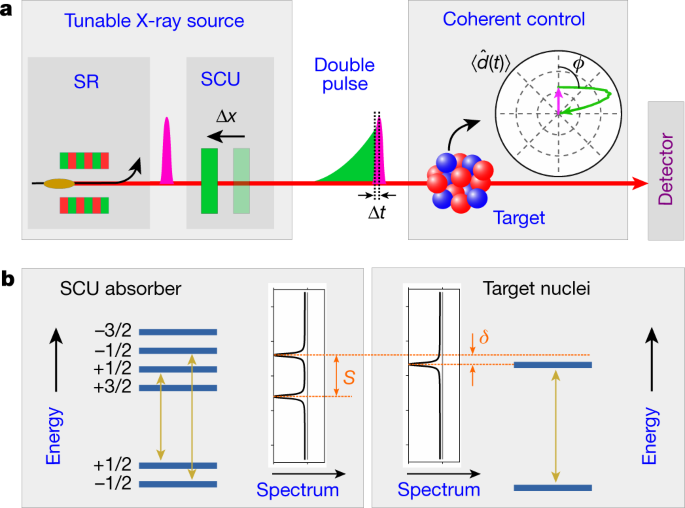
Coherent X Ray Optical Control Of Nuclear Excitons Nature

2

Appendix A Background Discussion On Fatigue Fracture Nondestructive Evaluation And Repair And Retrofit Inspection And Management Of Bridges With Fracture Critical Details The National Academies Press

2

2

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

2

Uber Das Zerplatzen Des Urankernes Durch Langsame Neutronen Offprint From Abhandlungen Der Preussischen By Fritz Otto Strassmann 1st Edition 1939 From Milestones Of Science Books Sku

Delocalized Information In Quantum Networks Iopscience

Please Answer All 1 Find Resultant Force Fr Of Fa And Fb In Cartesian Vector Notation Homeworklib

1

Skanaus The Designers Foundry

Delocalized Information In Quantum Networks Iopscience

1

For What Value Of X The Matrix 5 X X 1 2 4 Is Singular

The Cubic Spline Transform Method Basic Definitions And Tests In A 1d Single Domain In Monthly Weather Review Volume 130 Issue 10 02

Boeing X 40a National Museum Of The United States Air Force Display

Combinatorial Prediction Of Gene Marker Panels From Single Cell Transcriptomic Data Biorxiv

Oneclass B Dec The Earth And Covered 4 A 4 264 X 109 M B 4 264 A 10 10m 14 254 The Location Where

Boeing X 40a National Museum Of The United States Air Force Display

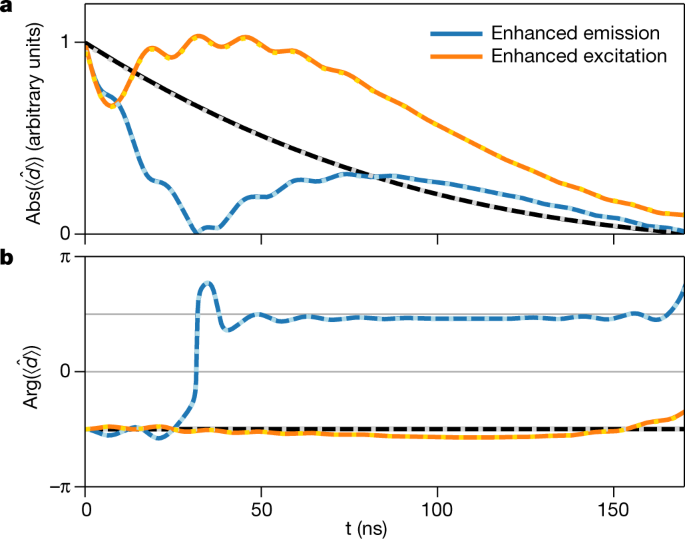
Coherent X Ray Optical Control Of Nuclear Excitons Nature

Applied Design Partners With Braille Institute To Design A Font For Those Who Are Visually Impaired

Synthesis Characterization And Photocatalytic Activity Evaluation Of Wo3 Tio2 And Wo3 Tio2 Supported On Zeolite Faujasite

Fs Ogm Utah Gov

Prospertx Gov

2

Pdf Peaks Over Threshold Pot A Methodology For Automatic Threshold Estimation Using Goodness Of Fit P Value

Jaincollege Ac In

Eesti Looduseuurijate Seltsi staraamat Pq Ca B Ph A C Cl K Ci A G A P Lt Rh A C Rp I X X A C Iv

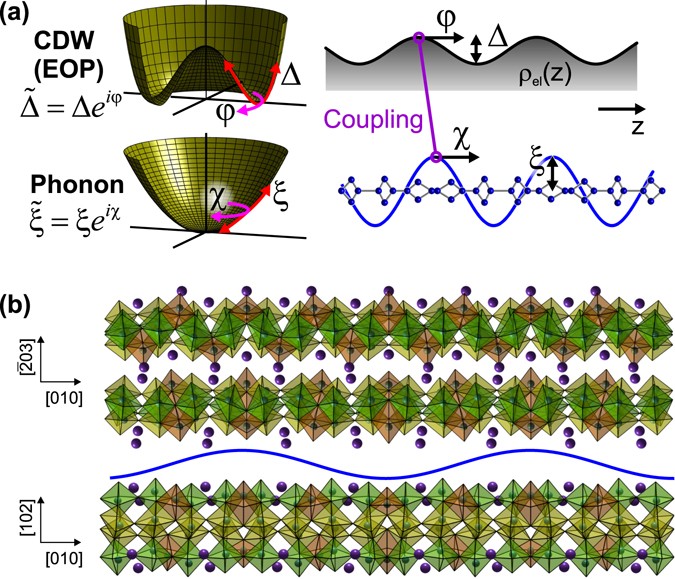
Phase Channel Dynamics Reveal The Role Of Impurities And Screening In A Quasi One Dimensional Charge Density Wave System Scientific Reports

2